如何选取最合适的预训练模型(3)
前言
上两篇文章我们分别讲解了LogME和DISCO的原理以及实验小结论。诚然,这两种方法都有效的展示了基础模型和数据之间的关系,LogME直接的利用贝叶斯边际似然的方法,给不同的基础模型打分;DISCO细致的观察不同奇异值和分类分数之间的关系,更细粒度的展示了基础模型微调前后的变化,后续的实验也验证了它们的准确性。
然而,我们依旧对微调这件事有些茫然。具体来说,我们只通过微调时奇异值的流动变化和分类的分数变化观察到了一些现象,并且这些小结论都是符合直觉的。因此,为了更加细致的理解微调这件事,我们可以引用一个全新的概念:learning dynamics。正巧,它正是通过观察$\textcolor{magenta}{\theta}$的变化,理解$\textcolor{magenta}{f_\theta}$的变化。
关于learning dynamics,一篇非常有技术含量的文章正讲解了这一概念面对大语言模型微调的理论分析。在这里,我们将尝试利用类似概念处理时间序列基础模型,以进一步思考和分析微调的整体过程。
对learning dynamics的定义
定性来说,learning dynamics主要在做特定训练示例的学习如何影响模型对其他示例的预测。这面对分类问题将会非常适合。首先,我们先定义一些变量:$\textcolor{magenta}{\theta}$表示模型参数,$\textcolor{magenta}{f_\theta}$表示模型函数。这样,问题的定义就会变成:$\textcolor{magenta}{\theta}$的变化如何影响$\textcolor{magenta}{f_\theta}$的变化
显然,无论是深度学习还是基础模型的微调,都将用到梯度下降。在这里我们引入梯度下降,以定量分析整个过程:
\[\textcolor{magenta}{\theta_{t+1} - \theta_t = -\eta\,\nabla_{\!\textcolor{magenta}{\theta}}\,\textcolor{magenta}{\mathcal{L}\!\bigl(f_{\textcolor{magenta}{\theta}}(x_u),\,y_u\bigr)}}\] \[\textcolor{magenta}{\Delta f(x_0) = f_{\theta_{t+1}}(x_0) - f_{\theta_t}(x_0)}\]在这里,$\textcolor{magenta}{\eta}$表示学习率,$\textcolor{magenta}{\mathcal{L}!\bigl(f_{\theta}(x_u),\,y_u\bigr)}$表示损失函数,$\textcolor{magenta}{x_u}$和$\textcolor{magenta}{y_u}$表示输入的样本对。紧接着,问题变为梯度更新后,模型的预测会如何发生变化
就此,我们先考虑一个标准的监督学习模型,也就是$\textcolor{magenta}{x}$经过模型学习映射到$\textcolor{magenta}{\mathbf{y} = {y_1, \ldots, y_L} \in \mathcal{V}^L}$这样的多分类问题,一般是先生成logits矩阵$\textcolor{magenta}{\mathbf{z} = h_\theta(\mathbf{x}) \in \mathbb{R}^{V \times L}}$,再通过每列计算softmax得到概率分布,取对数可以得到:$\textcolor{magenta}{\log \pi_\theta(\mathbf{y} \mid \mathbf{x})}$
对上面的对数进行learning dynamics的分析:
\[\textcolor{magenta}{ \Delta \log \pi_t(y \mid x_0) \triangleq \log \pi_{\theta_{t+1}}(y \mid x_0) - \log \pi_{\theta_t}(y \mid x_0) }\]从最简单的1分类,也就是$L = 1$的情况,我们可以将上式分解为:
\[\textcolor{magenta}{ \Delta \log \pi^t(y \mid x_o) = -\eta \cdot \mathcal{A}^t(x_o) \cdot \mathcal{K}^t(x_o, x_u) \cdot \mathcal{G}^t(x_u, y_u) + \mathcal{O}(\eta^2 \|\nabla_\theta z(x_u)\|_\text{op}^2), }\]具体的推导的过程鉴于篇幅就不详细列出了,可以直接看原论文的附页部分。
| 这个式子的$\textcolor{magenta}{\pi = softmax(z)}$,$\textcolor{magenta}{z = h_\theta(x)}$,$\textcolor{magenta}{\eta}$表示学习率,$\textcolor{magenta}{\mathcal{A}^t(x_o) = \nabla_z \log \pi_{\theta^t}(x_o) = I - \mathbf{1}\pi_{\theta^t}^\top(x_o)}$, $\textcolor{magenta}{\mathcal{K}^t(x_o, x_u) = (\nabla_\theta z(x_o) | {\theta^t})(\nabla\theta z(x_u) | _{\theta^t})^\top}$ 是关于z的经验神经正切核(eNTK), 然后 $\textcolor{magenta}{\mathcal{G}^t(x_u, y_u) = \nabla_z \mathcal{L}(x_u, y_u) | _{z^t}}$. |
自此可以发现:
$\textcolor{magenta}{\mathcal{A}^t(x_o) = I - \mathbf{1}\pi_{\theta^t}^\top(x_o)}$仅和模型当前的预测概率$\textcolor{magenta}{x_o}$有关;
$\textcolor{magenta}{\mathcal{K}^t(x_o, x_u)}$ 可以理解为不同输入样本之间对模型的相似性测量,也就是说如果$\textcolor{magenta}{\mathcal{K}^t(x_o, x_u)}$ 的F范数越大,就说明$\textcolor{magenta}{x_u}$的更新会对$\textcolor{magenta}{x_o}$的预测有更大的影响;
$\textcolor{magenta}{\mathcal{G}^t(x_u, y_u)}$和损失函数有关
关于Learning Dynamics的一些小实验:
的确,上面的理论分析有些复杂,但我们至少有一些共识,learning dynamics成功的将模型的变化情况进行分解,更有利于分析模型内部的变化情况。那么我们通过一些实验直观发现这一有趣理论:
我们利用第二篇文章给出的实验条件,分析该方法在Mantis模型上微调的结果,这里由于learning dynamics需要较长的时间进行分析,故我选择了每10个epoch分析,一共微调50epoch,并仅使用数据集的10%进行训练,20%用于测试
首先观察输出结果:
1
2
3
4
5
6
7
8
9
10
11
12
============================================================
NTK LEARNING DYNAMICS ANALYSIS SUMMARY
============================================================
A-Matrix PSD Ratio: 1.0000
Total samples analyzed: 45000
Final training accuracy: 0.9800
Final training loss: 0.0650
Analysis points: 450
Probability paths tracked: 100
Path length (analysis steps): 450
Analysis results saved to: mantis_ntk_analysis
============================================================
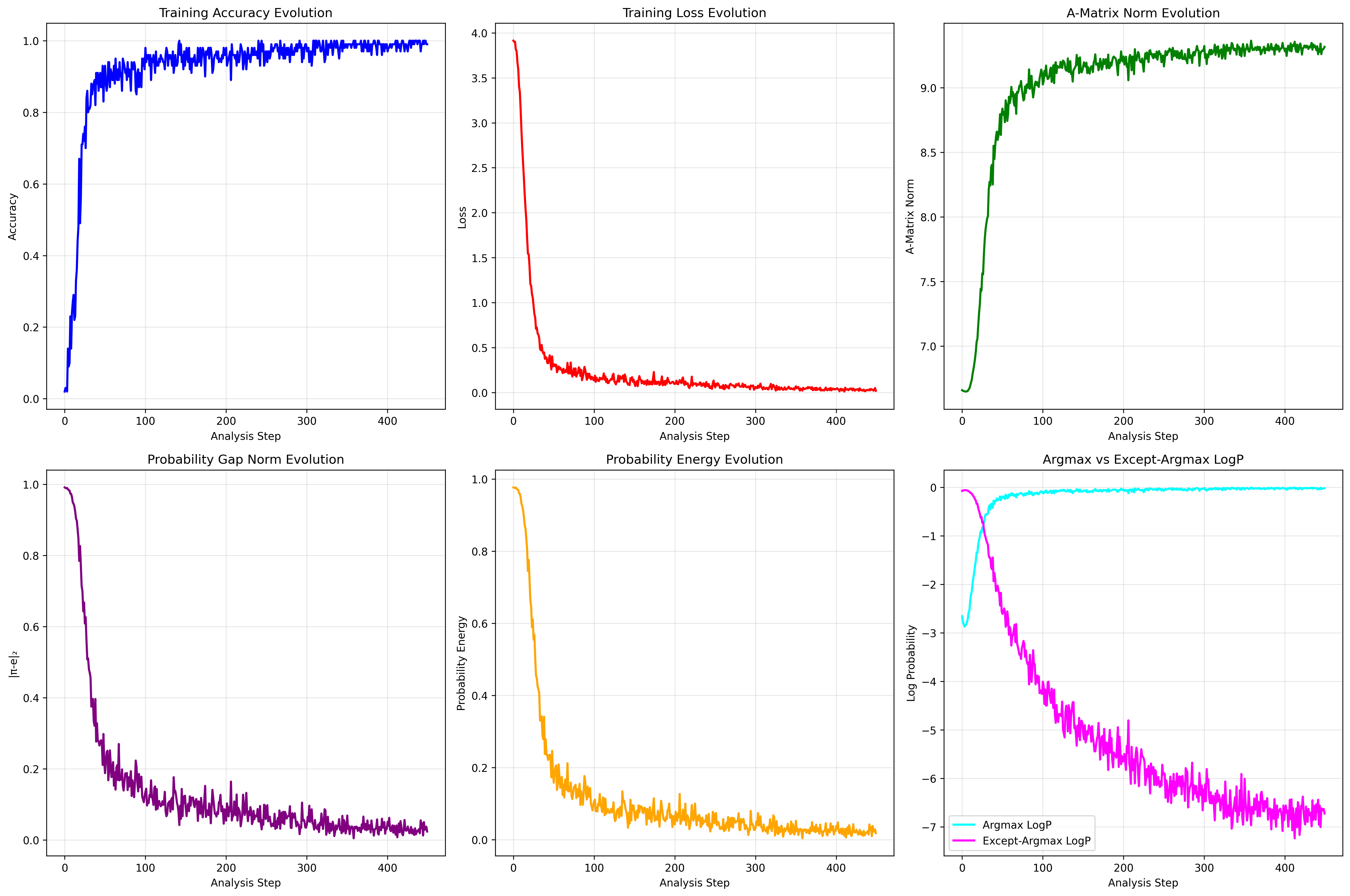
Mantis的微调结果很好自不必说,我们同样可以发现:450 步内,A 始终正定,Trace 指数衰减,Loss 线性下降,轨迹直线漂移,完全符合 AKG 线性动力学预言。
可以看到我们仅分析了A矩阵的learning dynamics,因为K和G在大模型中根本难以计算,大模型内部有很多模块,其中的梯度更新损失更新都是十分复杂的,因此只能从模型输出的A矩阵进行分析。不过好消息是,即使是A矩阵也足够有价值和信息供我们分析大模型的内部变化情况。
除了常见的损失和准确率,这里新加了更多的指标:
欧几里得距离 \(|\pi - e|_2 = \|p(y|x) - e\|_2 = \sqrt{\sum_i (p_i - e_i)^2}\)
归一化项 (A_{\text{norm}}) \(A_{\text{norm}} = \sqrt{V \cdot \|p\|_2^2 + (V - 2)}\)
能量函数(Energy) \(\text{Energy} = 1 - p(y^* | x)\)
最大概率的对数(Argmax Logps) \(\text{Argmax Logps} = \log\bigl(p(y_{\text{max}} | x)\bigr)\)
非最大概率的对数(Except-Argmax Logps) \(\text{Except-Argmax Logps} = \log\bigl(1 - p(y_{\text{max}} | x)\bigr)\)
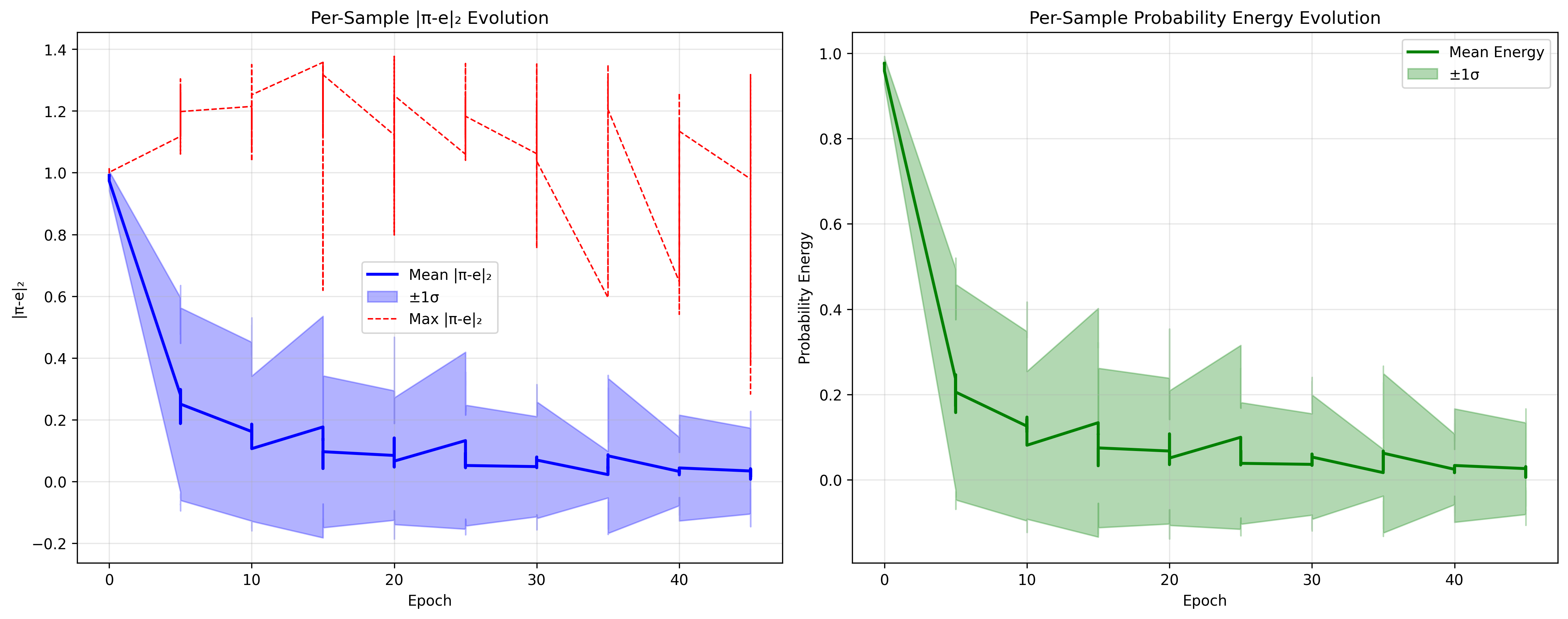
在这些指标里,最有意义的是欧式距离,因为它可以根据距离的远近得到样本的不确定度,大概是这样的输出:
1
2
3
4
5
6
7
8
9
10
11
12
13
Most Uncertain Samples (Top 10):
Sample Index | |π-e|₂ Value
------------------------------
73 | 0.7352
78 | 0.6376
44 | 0.4283
40 | 0.4070
32 | 0.3231
33 | 0.2492
52 | 0.0872
13 | 0.0615
0 | 0.0463
70 | 0.0386
当然,更细节的每个样本里都有对每个类别的不确定性量化:
1
2
3
4
5
6
7
8
9
10
11
Sample 73:
1. Class 38: 51.54%
2. Class 40: 47.56% (TRUE)
3. Class 42: 0.19%
4. Class 15: 0.18%
5. Class 35: 0.13%
6. Class 17: 0.12%
7. Class 13: 0.06%
8. Class 28: 0.04%
9. Class 10: 0.02%
10. Class 9: 0.02%
这大概对工业界而言是有帮助的,因为可以筛选出最不确定的10个样本,着重进行人工审核,其余的样本完全可以交给模型。可以看图片再直观理解:
learning dynamics不仅能理解模型、给出不确定性量化,还可以进行高质量的数据集筛选。对于这类方法,在LLM中已经有很不错的工作,可以参考这篇文章,那么同理,在时序基础模型中,同样可以采用这种方法,筛选出更高质量的数据集用于微调。
说的再详细点,前面learning dynamics的推导完全是对模型的输入和输出进行分析。那么对于高质量数据选择,就是去找损失下降最快的样本,也就是观察每一batch下的learning dynamics,再加权起来就好,具体的数学推导可以看文章。
总结
关于这个系列,后续会继续跟进并随机输出些我的记录。基础模型作为目前大模型的骨架,依然有很多值得深挖的点,包括它如何用于各个领域,以发挥其优势。