An Overview of Artificial Intelligence Applications for Power Electronics
前言
这篇整理算是回归老本行，AI4PE这个领域十分交叉，既要熟悉计算机领域的内容，还要对电力电子有着深刻的理解，或许和我本科学通信蛮有较大的关联度。本篇的整理源自2020年发表的一篇综述，由于AI领域的迅猛的发展，综述里许多AI的技术在目前看来已经较为古老。但从电力电子领域的角度来看，我们的最终目的是利用AI处理这里的问题。因此，AI的方法可以迭代更新，但电力电子领域内的问题依旧变化不大。
因此，本篇既是内容的整理，又是基于下一代AI技术应用电力电子的思考和展望。诚惶诚恐，我依旧不敢说我的思考有多么前瞻性，我十分喜欢将每一篇博客假想为起到了抛砖引玉的作用，同样我也相信，个人的眼光永远比不过群策共力，也许我的一个小的思考带动了更多人的思考呢？这，也大概是我喜欢记录的原因。
Introduction
电力电子这个大领域，我们可以分为三个小领域：design(设计)、control(控制)和maintenance(维护)。由于和工业联系紧密，因此这个领域非常注重实用性，且应用很广泛，包括功率模块散热器设计优化、多色发光二极管、风能转换系统等等。这些领域若要使用AI方法，可以分为优化、分类、回归和数据结构探索四个模块：
优化：例如在设计领域，我们需要探索一组最佳参数的工具，这些参数在设计的约束下最大化或最小化设计目标。这在本质上便是优化问题；
分类：例如维护领域的异常检测、故障诊断；
回归：其目的在于识别输入变量和目标变量之间的关系，也就是给定输入变量，预测一个或多个目标变量，例如对于功率半导体的剩余寿命预测问题，本质就是回归好，才能预测；
数据结构探索：从数据角度探索数据间的关系，例如从高维到低维，但在目前的研究中，数据结构探索一般是第一步需要解决的问题。
那么AI方法有哪些呢？当前综述介绍了专家系统、模糊逻辑、元启发式和机器学习四大方法。但目前的AI方向发展迅速，已经被各种大模型占据，因此我们从大模型这个角度出发来探索它在电力电子中的应用。目前来看大模型具有如下几大特点：
泛化性强：这意味着仅需少量的数据就可以达到很高的准确率，在维护领域中的故障诊断、异常检测可以完美发挥它的优势；
可生成式：利用自回归方式进行预训练的大模型，可以生成各种文本、代码、音频等数据模式，这意味着可以利用大模型处理设计领域的问题：给定约束和目标来自动生成符合要求的最佳参数；
多任务式：一般大模型可以处理各个下游任务，这意味着我们无需寻找特定的模型来处理每个任务，而只需微调大模型即可；
可扩展性：大模型具有scaling law这一神奇法则，它代表当我们找到合适的模型后，仅需要增大模型参数、或增大数据量，即可让下游任务的准确率不断提升；
多模态：可以通过需要来输入各种类型的数据：时序信号、图像、文本等，同样输出也可以是多模态的。
……
大模型本身仍处于发展阶段，上述的特点也仅是目前已被验证的能力，未来应该能被探索出更多有趣的特点。接下来，我们从design(设计)、control(控制)和maintenance(维护)三个角度分别思考大模型如何应用：
Design
设计领域的任务包括拓扑选择、元件尺寸、电路合成、可靠性考虑等任务，本质上属于优化问题，一般流程包括如下四个步骤：
- 目标制定：也就是最大化或最小化理想设计目标，包括元件参数、质量、面积、成本、散热片布局等。需要先将期望的设计要求明确表述为单一目标函数或多个目标函数，如下所示：
其中 $g(x)$ 为不等式约束，$h(x)$ 为等式约束， $x$ 为设计变量，$f(x)$ 为目标函数， $w$ 为权重向量，$x_l$ 和 $x_u$ 为设计变量的下界和上界，这里可以利用帕累托前沿来确定最优解。
约束空间：定义目标函数所受到的可行空间限制，一般源自实际情况
解决方案探究：优化方法是通过调整决策变量来最大化\最小化目标函数的
性能评估：候选解决方案可通过仿真、硬件在环测试、原型实验等方法，针对预定义的目标进行测试。测试结果可反馈至前一阶段，以进一步提升性能并进行优化。
整体的流程就是一个迭代试错过程，基于评估结果来优化其中的部分。这种方法的弊端就是耗时、需要专业人员评估、流程繁琐。当然，综述中提到可以通过人工智能方法缓解。主要应用于1.目标函数的建模以缩短设计时间和3.解决方案的探索以提升建模与优化效果。
在这里，大模型将会起到更大的作用。由于设计领域整体的流程是自动的，且迭代试错非常类似代码面对问题的处理过程，因此一类的研究尝试将LLM融入设计领域进行指导。例如PE-GPT通过从电力电子的知识库中进行检索增强生成（RAG）方法来增强PE-GPT，并提出了一个混合框架，将LLM代理与元启发式算法、模型动物园和模拟存储库集成在一起。这增强了其多模态处理能力，并实现与现有设计工作流程的集成。该方法通过双有源桥（DAB）转换器的调制设计和降压转换器的电路参数设计进行实验，并发现与人类专家相比，PE-GPT的正确性提高了22.2%。与其他领先的LLM相比，PE-GPT的正确性提高了35.6%，一致性提高了15.4%。
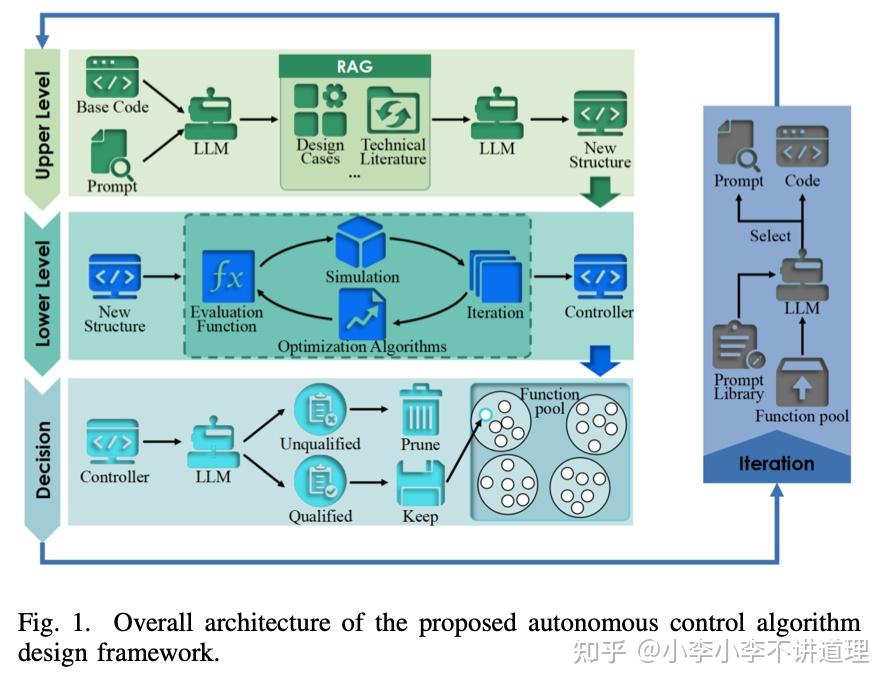
还有GenControl利用LLM的生成能力，智能探索和迭代改进控制算法的结构，并利用粒子群优化（PSO）算法有效地完善任何给定结构的参数。这种方法实现了端到端的自动化设计，通过模拟DC-DC Boost转换器进行验证，成功地将基本控制器演变成高性能自适应版本
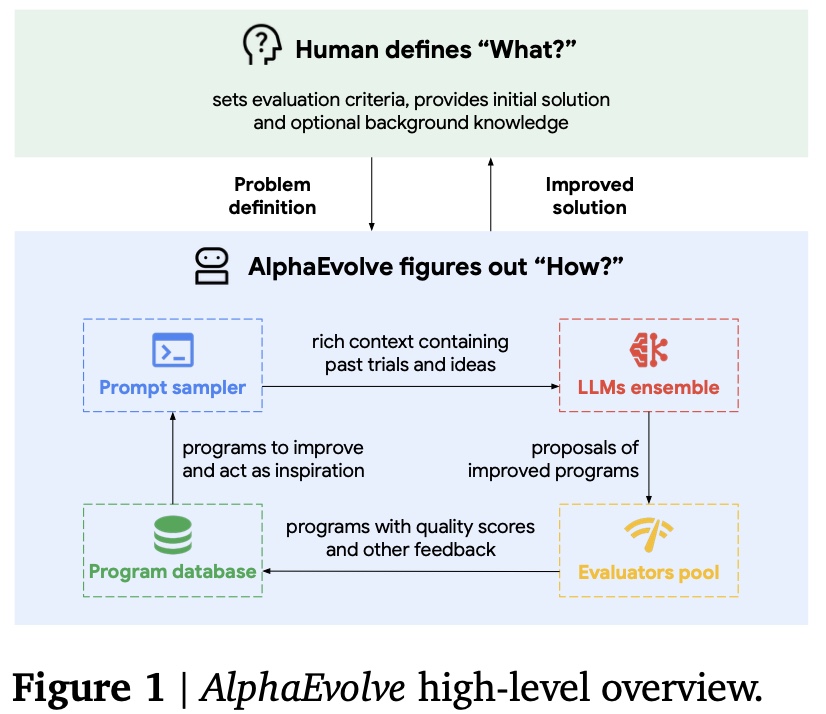
同样，目前很热门的AI Agent也值得我们探究，因为其本质仍是利用LLM进行各种自动化的流程设计。例如DeepMind提出的AlphaEvolve。它大大增强了最先进的LLM在解决开放科学问题或优化计算基础设施的关键部分等极具挑战性的任务上的能力。它使用进化方法，不断接收来自一个或多个评估者的反馈，迭代改进算法，从而有可能带来新的科学和实际发现。这个流程十分类似电力电子领域的设计流程。
但说到底，这些仅是对大模型的基础尝试，并且LLM主体仍是文本的输出，这和电力电子的设计领域并不搭。因此，我们更需要思考，如何做出属于我们电力电子领域的“基础”模型。诚然，在目前看来这是费钱费力的事情，但其余相关领域已经给出一些设计范式，启发我们更多的思考：
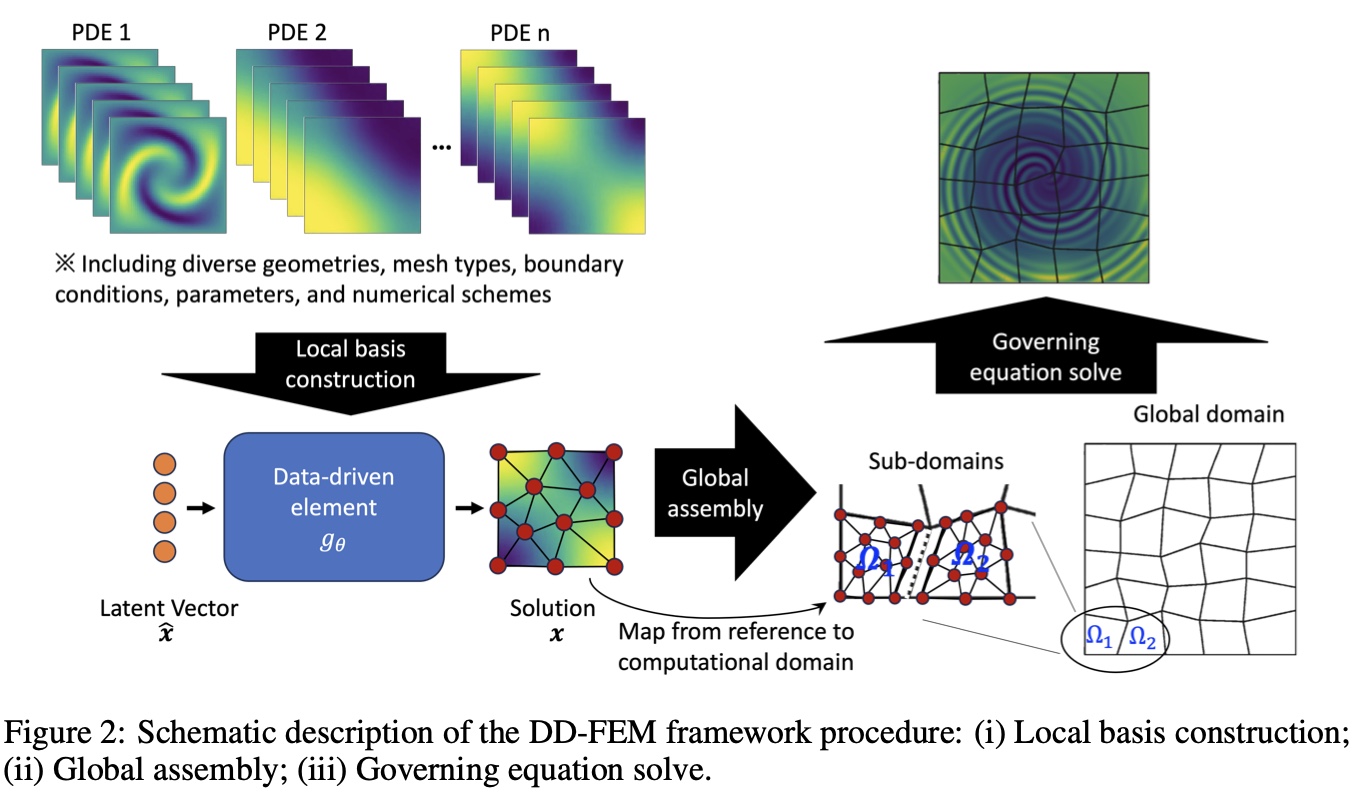
例如，计算科学领域的DD-FEM，非常巧妙的将有限元方法和大模型结合起来。有限元方法本就将把求解PDE/ODE，这种连续的求解区域离散为有限数量的单元和节点，通过定义在节点处的基函数来近似原始的连续解函数。这正和LLM中的设计类似，全局域划分为更小的子域类似LLM的分词；组装局部基函数构建全局解类似LLM的推理过程。
但我个人认为，大模型的生成能力更值得关注。这里的生成能力并非LLM中的文本生成，而是直接可以生成最优理想方案的生成能力：给大模型输入相关参数和约束，它可以直接推理生成最理想的设计目标。这在材料的设计领域已经有初步的工作：MatterGen自主创建了生成式大模型，通过在给定所需的属性约束下直接生成新材料来加速材料设计。MatterGen产生的结构是新的和稳定的可能性的两倍以上，并且接近局部能量最小值的十倍以上。经过微调后，MatterGen可以产生了具有所需化学、对称性和机械、电子和磁特性的稳定新材料。这在本质上也属于设计的“存在性”问题。
Reliability-oriented design (ROD)
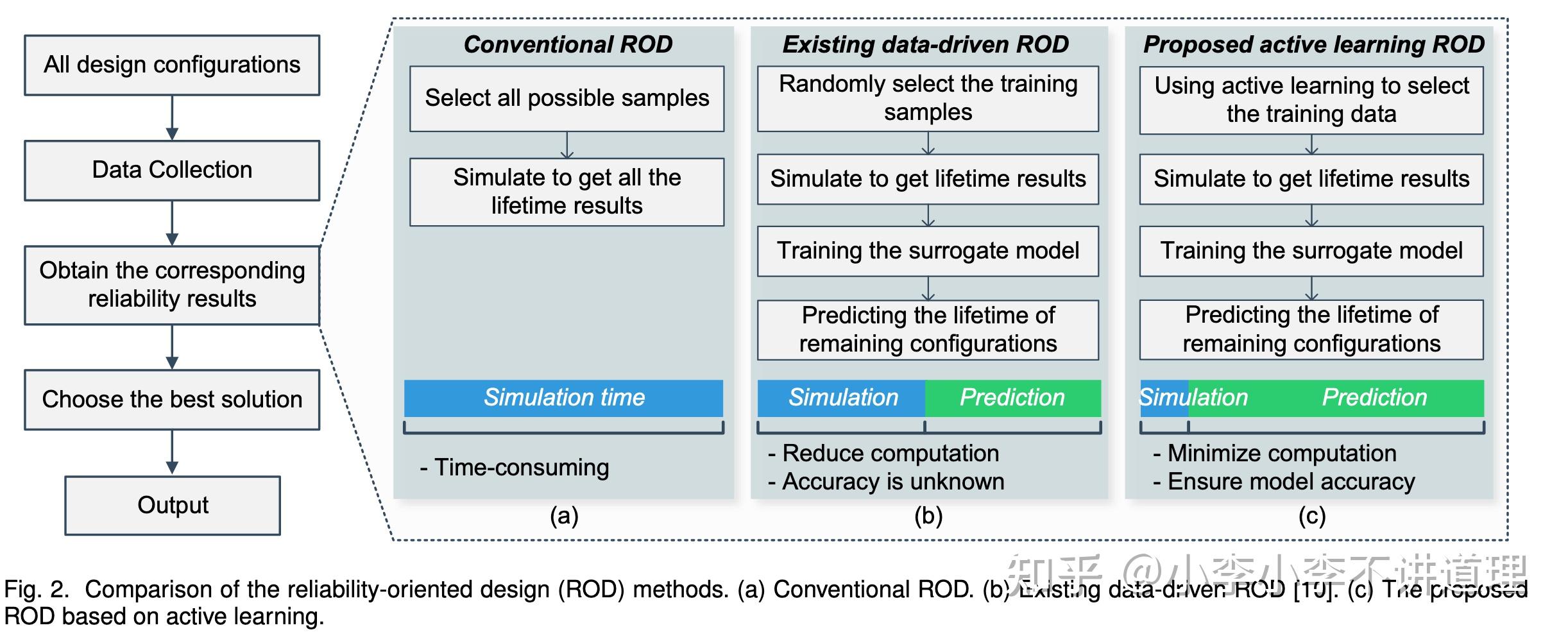
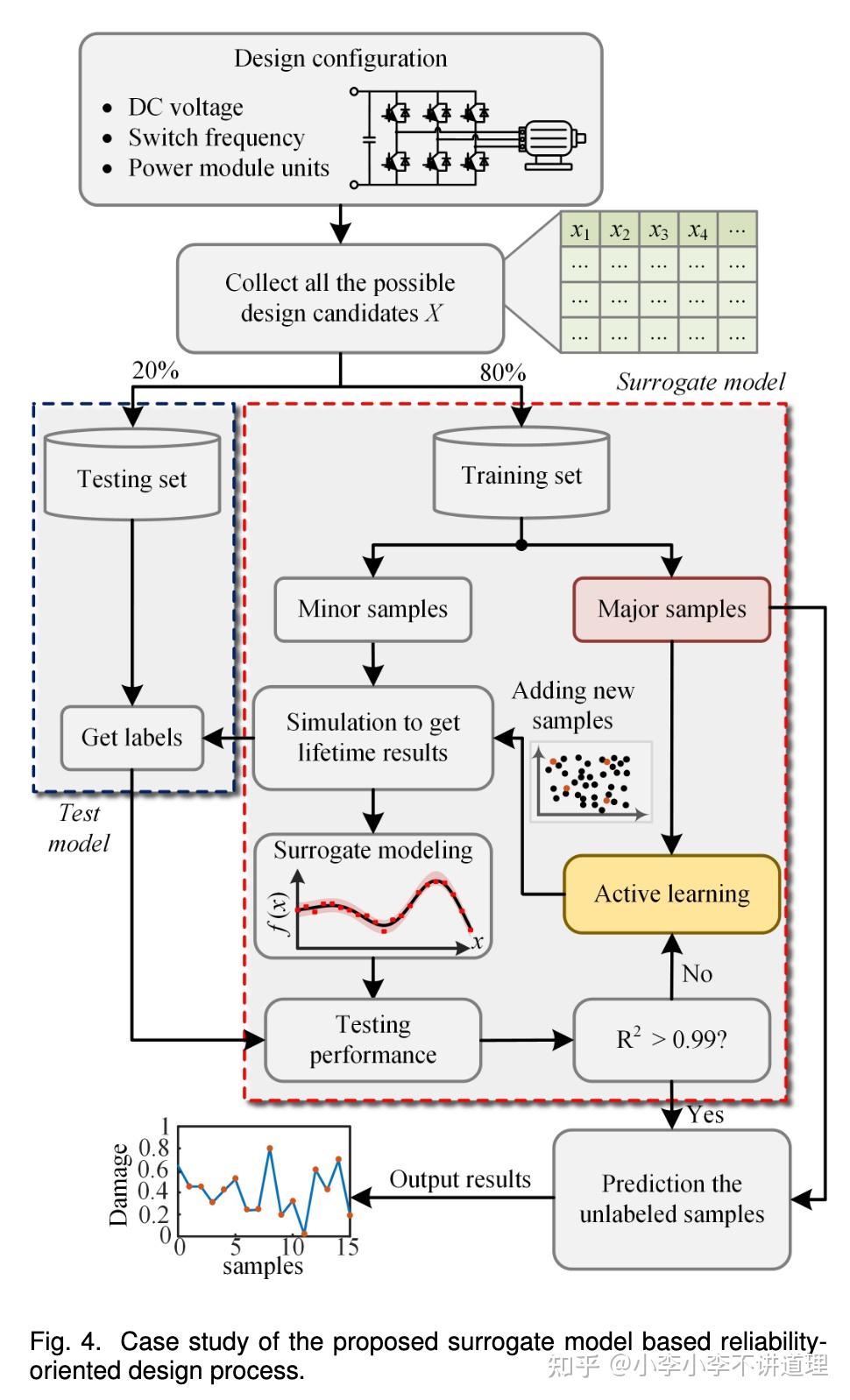
这里着重讲一下可靠性导向设计。其做法是对每个候选的设计进行可靠性评估，如下图所示。
传统的ROD方法严重依赖于对大量潜在候选设计的广泛仿真和可靠性评估。例如，所有电路参数（例如开关频率、电压等）和不同的元件选择都会影响可靠性，但庞大的计算要求和有限的外推能力使这种传统方法不切实际。
而现有的数据驱动的ROD方法已经提出。设计参数与可靠性性能之间的关系由基于仿真和测试收集的数据的替代模型表示。这种方法的计算效率更高，可以在短时间内探索更广泛的设计空间，但需要大量的标记数据进行训练。因此，主动学习这一框架应运而生。
如上图所示，这篇文章就详细介绍了如何利用主动学习找到最适合训练的样本，大大提高了数据的利用率。但我们仍可以观察其本质：它的目的便是利用少量标记的数据以实现高效训练，因此，大模型的泛化性便可以派上用场。预训练好的大模型本身就学习到了通用知识，仅需少样本微调即可实现高效训练。更有趣的是，上述提到的主动学习仍可以继续使用。大模型微调时也可以理解为训练模型，只是在一个更高的“起点”上训练（有效的通过预训练得到的初始化），它同样需要找到适于微调的数据，即可实现Less is more。
另外，关于代理模型，该文章使用的是高斯回归过程来近似目标输出，输出函数为高斯概率分布。我们依旧可以寻找更迅速的代理模型。例如SLIM-KL这篇文章采用了新型的高斯过程线性多核和通用稀疏感知分布式学习框架来优化超参数，使其更高效。这个角度仍将会有许多新的发现。
Control
控制器作为电力电子很重要的组成部分，人工智能对其的应用也主要分为优化和回归两类问题。与设计阶段的优化类似，控制应用程序中与优化相关的任务同样可以利用大模型的生成能力处理，因此这里不再过多赘述。我们将目光的核心放到回归问题中。
面对回归问题，我们需要考虑以静态还是动态的方式处理系统输入和输出的非线性映射。直到目前，这个阶段仍存在一些局限：
- 控制器的配置需要深入了解系统控制原理，但这在复杂的实际情况来说具有挑战性，甚至不可行。对于复杂系统而言，考虑时变和分段线性特性非常耗时，其中控制器通常在几个关键点而不是整个区域进行优化，从而导致解决方案次优。也就是面对这样的长尾问题应该如何解决。
- 一旦控制器加载好，就会以静态方式运行，适应性有限，这表明它仅适用于时不变系统。然而，当环境和条件发生变化时，控制器对系统参数变化的鲁棒性会降低，控制性能可能会下降。
- 理想的控制器必须能够以快速瞬态响应来应对参数容差，以保持系统稳定性。然而，这种期望的功能无法很好地实现。
针对问题1和问题3，原本的综述介绍了Neural Network（NN）的应用、和Fuzzy logic的结合、RNN、LSTM的应用。NN作为一种强大的非线性映射工具，已经被广泛应用于控制领域。当然，近五年来模型架构的更新更是快速席卷，旨在高效的处理上述的问题。
Physics-informed Machine Learning
结合物理信息的机器学习方法（PIML），其原理就是在模型训练时加入显式的物理约束，以此加快模型进行参数估计，以更快的速度应对参数容差。在这里我们以dc-dc buck conventer为例：
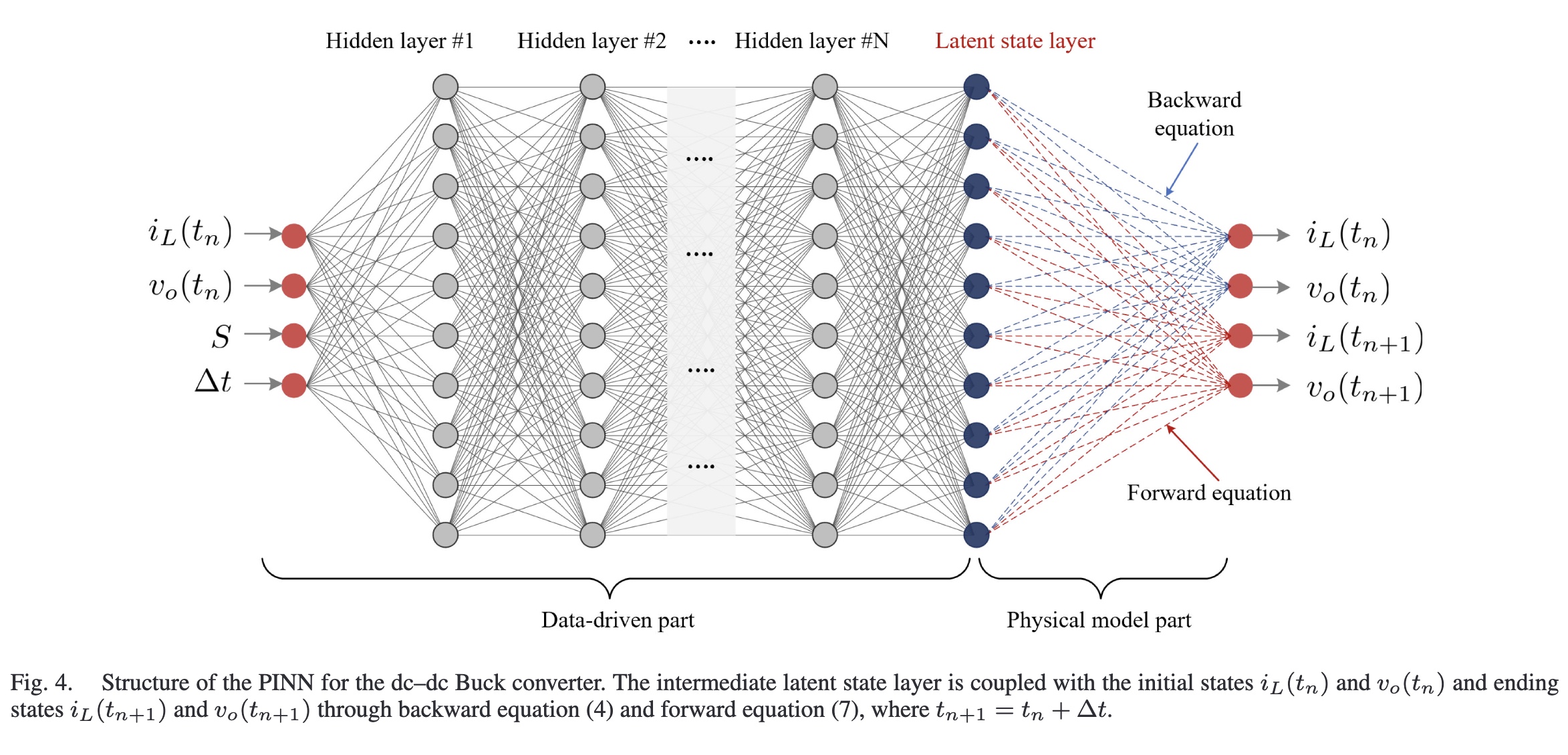这里的输入是电感电流、输出电压的初始状态、开关状态和从初始到初始阶段的时间段，数据驱动的输出是电感电流的中间潜态和输出电压，这些都是不可观测的，用作物理模型部分的输入，通过NN的深度学习即可学习；重点在于物理部分的处理。
More innovative model architectures
从综述中可以看出，计算机领域的模型架构更新时刻影响着人工智能应用电力电子领域的发展。直到目前，模型的架构正向着更快、更简约、复杂度更低的方向发展，这正契合着目前控制领域的局限。在这里将介绍一些对我们有启发的模型架构，以尝试将更高效的模型同电力电子结合起来。
在介绍这些崭新模型之前，我们需要先了解目前模型的发展情况。总结来说，从Transformer开始，目前可以讲模型架构发展分为三个阶段：
- Linear attention，其核心在于使用标准内积$k^Tq$来计算注意力权重，而不是使用softmax的幂$exp(k^Tq/sqrt{D_k})$，以此会产生输出$y_t \propto \sum_{i=1}^{t}v_i{k_i}^Tq_t$。在递归后更新矩阵状态$M_t=\sum_{i=1}^{t}v_i{k_i}^T$，整体的式子就可以写为：
同样，为了进一步拓展内积的表达，可以引入核函数策略：
\[M_t=M_{t-1}+v_t{\phi(k_i)}^T \\ y_t=M_t{q_t}=\sum_{i=1}^{t}v_i{\phi(k_i)}^T{\phi(q_t)}\]- State-space models and linear attention with forgetting，第一个矩阵$M_t$只能储存有限量信息，且它们一开始的平均加权会导致随着序列的增加，性能下降。于是加入了遗忘因子$\gamma _t$，只保留最新信息（是不是蛮像LSTM中的遗忘门），整体的式子可以更新为：
\(M_t=\gamma _tM_{t-1}+(1-\gamma _t)v_tk_i^T \\ y_t=M_t{q_t}\) 在每个步骤$t$中，$M_{t-1}$中所有先前的值都会衰减成$\gamma _t \in [0,1]$的因子，然后再存储新值。该策略也类似于state-space models（SSM）的序列层（Mamba, Mamba-2）中的遗忘因子，就是SSM中的时变步长和转换矩阵
- Fast-weight layers and test-time training layers，衰减所有过去信息除了刚提到的，还有只忘记旧键与新键$k_t$最相似的值。该方法的鼻祖就是DeltaNet，整体的式子如下所示：
关于deltanet及其系列模型，可以关注sonta小姐姐的文章和她的科普
鉴于篇幅所示，就不再过多赘述模型架构的总结，具体可看这篇文章：Test-time regression: a unifying framework for designing sequence models with associative memory，中文版可以看苏神写的博客：线性注意力简史：从模仿、创新到反哺
由于电力电子是时间序列，并且数据背后带有强物理背景，因此我们将目光聚焦到时间序列的崭新模型架构中，当然也得带有物理背景。在此推荐的第一个是LinOSS模型，其本质处于模型架构的第二阶段，但很有趣的是它将ODE方程稳定的离散化，并使用快速关联并行扫描随着时间的推移进行集成，产生了特定的状态空间模型，此外严格证明LinOSS是通用的，即它可以近似时变函数之间的任何连续和因果算子映射，达到所需的精度。从结果来看，它甚至超过了第二阶段的模型架构，可以处理超长时间序列模型。
如何应用呢？首先，电力电子中的控制器绝大多数都可以用ODE方程来描述，而LinOSS模型正可以高效处理。其次，LinOSS模型还可以用于处理时变系统，即系统的参数在不同时间点上会发生变化，这在电力电子中是常见的情况。例如，在DC-DC Buck Converter中，电感参数会根据开关状态的变化而发生变化，这就需要LinOSS模型能够自适应地调整模型参数，以保持模型的准确性。
DC-DC Buck Converter的连续时间ODE方程:
Buck 变换器分段线性状态方程（含 ESR）
定义
- 状态变量：
\(\mathbf{x} = \begin{bmatrix} i_L \\ v_C \end{bmatrix}\) - 输入变量：
\(u = V_{\text{in}}\) - 输出变量：
\(y = v_o\)
| 参数 | 含义 |
|---|---|
| $L$ | 电感量 |
| $C$ | 电容量 |
| $R_c$ | 电容等效串联电阻（ESR） |
| $R$ | 负载电阻 |
| $V_F$ | 二极管正向压降（同步整流时可设为 0） |
| $S$ | 开关函数：$S=1$ 表示导通，$S=0$ 表示关断 |
1. 开关导通阶段（$S=1$）
状态方程： \(\frac{d}{dt} \begin{bmatrix} i_L \\ v_C \end{bmatrix} = \begin{bmatrix} -\dfrac{R_c}{L} & -\dfrac{1}{L} \\[6pt] \dfrac{1}{C} & -\dfrac{1}{C(R_c+R)} \end{bmatrix} \begin{bmatrix} i_L \\ v_C \end{bmatrix} + \begin{bmatrix} \dfrac{1}{L} \\[6pt] 0 \end{bmatrix} V_{\text{in}}\)
输出方程： \(v_o = \frac{R}{R_c+R}\,v_C + \frac{R_c R}{R_c+R}\,i_L\)
2. 开关关断阶段（$S=0$）
状态方程： \(\frac{d}{dt} \begin{bmatrix} i_L \\ v_C \end{bmatrix} = \begin{bmatrix} -\dfrac{R_c}{L} & -\dfrac{1}{L} \\[6pt] \dfrac{1}{C} & -\dfrac{1}{C(R_c+R)} \end{bmatrix} \begin{bmatrix} i_L \\ v_C \end{bmatrix} + \begin{bmatrix} -\dfrac{V_F}{L} \\[6pt] 0 \end{bmatrix}\)
输出方程与导通阶段相同： \(v_o = \frac{R}{R_c+R}\,v_C + \frac{R_c R}{R_c+R}\,i_L\)
3. 紧凑写法（单公式）
引入开关函数 $S\in{0,1}$，可把两段合并为一条分段线性 ODE：
\[\frac{d}{dt}\mathbf{x} = \underbrace{ \begin{bmatrix} -\dfrac{R_c}{L} & -\dfrac{1}{L} \\[6pt] \dfrac{1}{C} & -\dfrac{1}{C(R_c+R)} \end{bmatrix} }_{\mathbf{A}} \mathbf{x} + \underbrace{ \begin{bmatrix} \dfrac{1}{L} \\[6pt] 0 \end{bmatrix} (S\cdot V_{\text{in}} - (1-S)\cdot V_F) }_{\mathbf{B}(S)}\]输出： \(v_o = \underbrace{ \begin{bmatrix} \dfrac{R_c R}{R_c+R} & \dfrac{R}{R_c+R} \end{bmatrix} }_{\mathbf{C}} \mathbf{x}\)